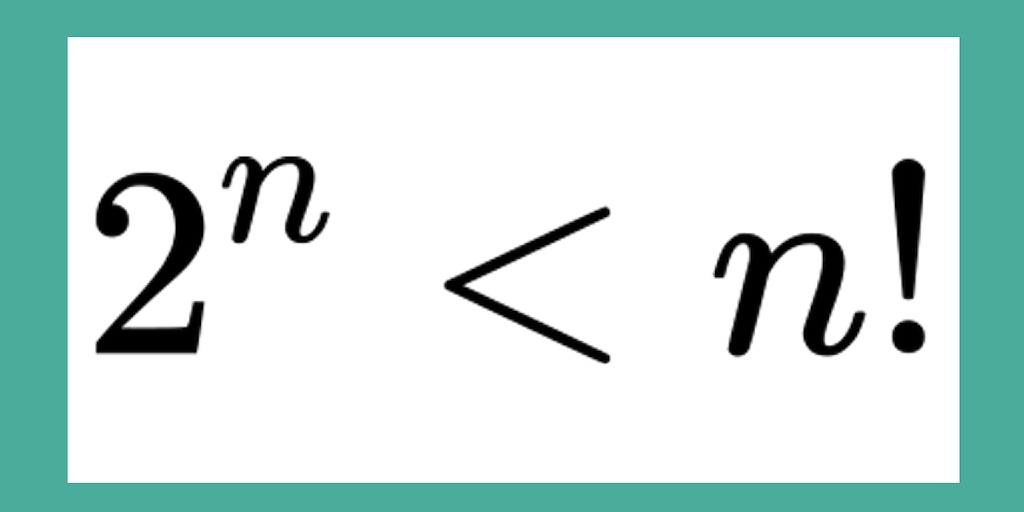
$4 \le n$ において2のn乗はnの階乗より小さいことの証明。
数学的帰納法による証明
$4 \leq k$ における自然数 $k$ が $2^k < k!$ を満たすと仮定する。
このもとで $2^{k+1} < (k+1)!$ が成り立つことを示す。
$2^k < k!$ より以下が成り立つ。
$$ (k+1)! = (k+1)k! > (k+1) \cdot 2^k $$
$2 < 5 \leq k+1$ であるから
$$ (k+1)! > 2 \cdot 2^k $$
すなわち $2^{k+1} < (k+1)!$
$n=k$ を仮定すると $n=k+1$ でも成立することが示せた。
以上、数学的帰納法より自然数 $n (4 \leq n)$ において $2^n < n!$ が成り立つ。
大小関係を利用した証明
分数にして分母分子を比較し、1との大小関係を示す。
$$ \frac{n!}{2^n} = \frac{4!}{2^4} \frac{5}{2} \frac{6}{2} \frac{7}{2} \cdots \frac{n}{2} > 1 $$
それぞれの分数を見ると、分母より分子が大きいので1より大きい。 そして、1より大きいものは何回掛け合わせても1より大きい。
すなわち $4 \le n$ において $2^n < n!$ が成り立つ。

